Probit Analysis

Probit Analysis is a specialized regression model of binomial response variables (variable with only two outcomes). It transforms the sigmoid dose-response curve to a straight line that can then be analyzed by regression either through least squares or maximum likelihood.
Applications of probit analysis

Probit Analysis is commonly used in toxicology to determine the relative toxicity of chemicals to living organisms. This is done by testing the response of an organism under various concentrations of each of the chemicals in question and then comparing the concentrations at which one encounters a response. Here, the response is always binomial (e.g. death/no death) and the relationship between the response and the various concentrations is always sigmoid. Probit analysis transforms the sigmoid to linear and performs regression on the relationship. There are many endpoints used to compare the differing toxicities of chemicals, but the LC50 (liquids) or LD50 (solids) are the most widely used outcomes of the modern dose-response experiments. The LC50/LD50 represent the concentration (LC50) or dose (LD50) at which 50% of the population responds.

The Estimation of the Median Effective Dose:

In Probit analysis successive batches of insects are exposed to different concentrations of the poison/chemical for a constant time and, after a suitable interval, the numbers dead and alive are recorded.

            The probit analysis transforms the experimental results in order to estimate µ and σ²  from the following equation.

                               (1)

The probit of the proportion P is defined as the probability P in a normal distribution with mean 5 and variance 1 i.e.  the probit of P is Y, where

                                     (2)

If equation (1) represents the distribution of tolerances of dosages, the expected proportion of insect killed by a dose x₀ is given by

                           (3)

Comparing (2) and (3) for P shows that the probit of expected proportion killed is related to the dosage by the linear equation

                                            (4)

By applying probit transformation, experimental results may be used to give an estimate of this equation, and the parameters of the tolerance distribution may then be estimated. The median effective dosage is estimated as that value of x which gives Y = 5

The Probit regression line

            There are two methods of estimation of the parameters i.e. graphical method or statistical process Both depend upon the probit transformation. The graphical approach is rapid and is sufficiently good for many purposes, but for some ore complex problems, or when an accurate assessment of the precision of estimates is needed, the second method is preferred.

Method – I (graphical Approach)

Ø Find out the least tolerated (smallest) dose (100% mortality) and most tolerated (highest) dose (0% mortality) by hit and trial method 

Ø Once these two doses are determined, select at least 5 doses in between them, and observe mortality due to these doses 

Ø Calculate the percentage kill observed for each dose and convert them to probit.

Ø Apply correction factor to 0% and 100% mortality group [for 0% dead = 100 (0.25/n) and for 100% dead = 100x (n-0.25/n), where n = number of death] 

Ø The percentage mortality values are converted to probit values by reading the corresponding probit units from the probit table 

Ø The probits are then plotted against x (the logarithm of the dose) and a straight line drawn by eye to fit the points satisfactorily as possible.

Ø The log LD 50 is estimated from the line as m (intercept), the dosage at which Y = 5.

Ø The slope of the line, b, which is an estimate of 1/σ, is obtained.

Ø These two parameters are then substituted in equation (4) to give the estimated relationship between dosage and kill.

Ø To test whether the line is an adequate representation of the data, a χ² test is performed.

Method 2 (Maximum Likelihood Estimation) (Procedure taken form Lei and Sun (2018)

1. Suppose in a population, n subjects are treated with doses (i) and r subjects show a response to each dose then the empirical proportion (p^*) of responders is given by

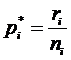                                                      (1)

where i = 1 to n and n is the number of doses

2. If we have a control group and response occurred in it with proportion C, the proportions of responders were corrected using the Abbott equation for each treatment dose

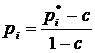                                                            (2)

3. The corrected proportion (p_i) was then converted to a probit value (y_i)

                                                (3)

where is inverse of Normal distribution

4. Establish a provisional regression line between y_i and the logarithm of the dose (x_i)

                               (4)

5. Calculate the expected probits (Y_i)

                                 (5)

6. Calculate  the expected response proportion (P_i) 

                (6)

where Φ(Y_i) is the cumulative probability of the standard normal distribution corresponding to (Y_i), and C is the natural response proportion if exist

7. Calculate the working probit (y_i) as

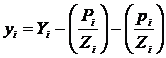,                  (7)

Where 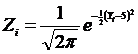              (8)

8. Compute expected probits from weighted regression of working probits weighted on x_i, with each y_i . A weight, n_iw_i,is assigned to each x_i and y_i where w_i is the weighting coefficient computed as

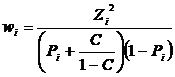                (9)

where C is the natural response of control group

9. The slope β of the working probit regression equation is given by

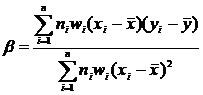         (10)

10. The intercept α of the working probit regression equation

,                                                (11)

Where 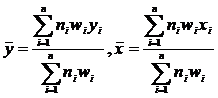      (12)

11. The standard error of β is

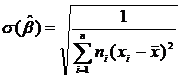                           (13)

and the standard error of α

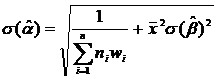                  (14)

12. The χ² statistic of the probit regression equation is computed as

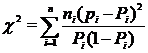                                   (15)

The significance level p of the χ² statistic can be calculated as the right-tailed probability of the chi-squared distribution with n – 2 degrees of freedom (d.f.).

A significant χ² statistic (p < 0.05) might indicate either that the population did not respond independently or that the fitted probit-log(dose) regression line did not adequately describe the dose-response relationship in the test samples.

To get an optimal fit of the probit-log₁₀(dose) regression, we substituted α and β for α₀ and β₀ and repeated the calculations of equation (5) to (15) until a stable χ² appeared, indicating convergence. This procedure is a maximum likelihood (ML) method

The significance of the slope was assessed using the z test 

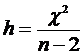                                                   (16)

If h < 1, the model provided a good fit to the data. Otherwise, standardized residuals will be plotted to identify outliers or other possible causes of poorness of fit. Each residual defined the difference between the observed r_i and the expected response number (n_iP_i) for each dose. The residuals were standardized by dividing them by their standard errors, . For models providing a good fit, the standardized residuals fell mostly between −2 and 2. Standardized residuals distributed randomly showed no systematic patterns or tendencies toward positive or negative sign.

Calculation of the lethal doses of toxicants or populations and their 95% CLs

In this step, we first calculated the logarithms of the doses (θ_π) at which levels of interest (π) gave the expected response proportion

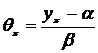                                                            (17)

where y_π was the π^th percentile of the probit distribution curve calculated in inverse of normal distribution for the probit distribution.

The π^th lethal dose was then calculated as

 and The standard error of θ_π, σ(θ_π) can be calculated as

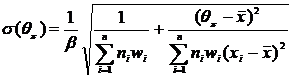           (18)

The 95% CL of the LD_π was then given as

10^θ_π±t_0.05,k−2σ(θ_π)                                                          (19)

Procedure to Perform Probit Analysis using Online Tool (OPSTAT)

Step 1: Enter the data of dose response in the text area provided or paste the data. The sequence of the data should be [dose][total no. of subject][No. of killed] in a single line corresponding to first dose. Enter the data for other doses in separate lines in the similar manner as above. In last line data for control group will be entered. as shown in example below

             Conc               No.      Killed
1.01               50        44
0.89               49        42
0.71               46        24
0.58               48        16
0.41               50        6
0                    50        0   

Step 2. Submit your data by pressing submit button.

Step 3. Enter the number of doses except control group in next page and press Analyse button.
The results will be displayed on separate webpage which can be printed or saved.

References

Ø Finney, D. J., Ed. (1952).Probit Analysis. Cambridge, England, Cambridge University Press.

Ø Finney, D. J. and W. L. Stevens (1948). "A table for the calculation of working probits and weights in probit analysis." Biometrika35(1-2): 191-201.

Ø Greenberg, B. G. (1980). "Chester I. Bliss, 1899-1979." International Statistical Review / RevueInternationale de Statistique8(1): 135-136.

Ø Hahn, E. D. and R. Soyer."Probit and Logit Models: Differences in a Multivariate Realm." Retrieved May 28, 2008, from http://home.gwu.edu/~soyer/mv1h.pdf

Ø Lei, C and Sun, X (2018). Comparing lethal dose ratios using probit regression with arbitrary slopes. BMC Pharmacology and Toxicology 19:61.